Another really good video from Chris Martensen at Peak Prosperity. I like his data-driven approach and wide-net data gathering. As far as I’m concerned he has consistently been one of the best voices on this subject from the beginning. We need more voices like his.
Again, I don’t necessarily subscribe to everything he says but the signal-to-noise ratio is extremely high.
Over the last couple of weeks, I’m getting convinced that the majority of infections are spread by a smaller group of super-spreaders, and that overall the general infectivity of Sars-CoV2 among the general population is much lower than initially thought. Analysis of the spread of S-CV2 between household members (which hovers around 10-13%) is part of the reason why I think that.
This has a direct effect on what the R0 for the disease is. The R0 is how many new people an average person infects. Currently estimates from Imperial College and others assume an R0 of approx 2.5 (Chris Martensen incidentally considers it to be much higher 4-6). The higher the R0, the more infectious the disease, and consequently the higher the percentage of people who need to be infected in order to reach herd-immunity.
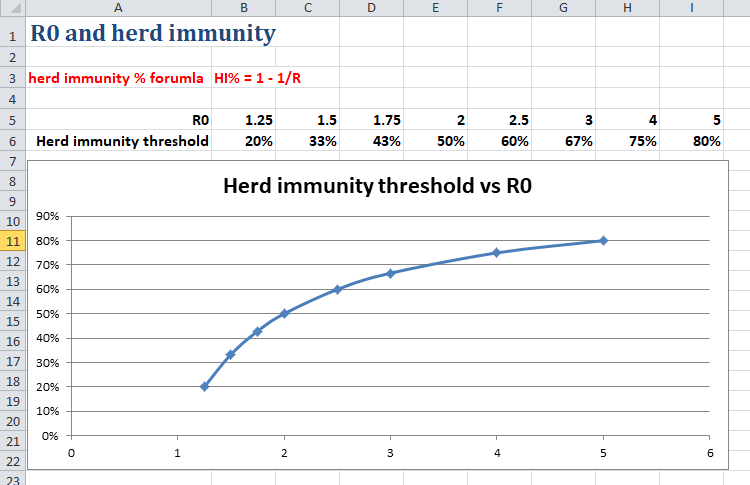
There is a simple formula that relates R0 and herd immunity:
infected pop for herd immunity = 1 - 1/R0
Taking the Imperial College R0 of about 2.5, that leads to the famous 60% number of people who need to be infected that was quoted by Chris Whitty and others in order to reach herd immunity.
That’s not exactly what we are seeing however. We see numbers of new cases petering off after about 10-20% infected (not everywhere it must be said). How come?
If it is true that a majority of the spread happens through super spreaders, and these folk catch the disease early, and then take themselves out of the equation, the R0 will start to evolve to a much lower level. What does that do to the idea of herd immunity?
From the chart above, it becomes clear that if the true value of R0 absent super-spreaders is closer to 1.5, we can expect to reach herd immunity at around only 33% of an infected population.
I don’t know what the true R0 is, but this has great implications in how we might start planning to control the ultimate spread of the disease and what sort of policies we might put in place.
Incidentally, the wearing of face masks in public places is also an important variable in the ultimate control of the R number, and hence the required number of recovered people to ultimately reach herd immunity.
Cheers
PP
In other news I notice in an interview* Bill Gates is saying that when a vaccine is finally dangerously unleashed safe and ready, it might be the case that only 30% of the population might need to have it. I mention him only as the standard bearer of the mainstream vaccine crowd. This ties in with an R0 of about 1.5 or so…
Interesting. I think the reason that folk are moving so quickly with this vaccine is that if they’re not careful the disease could burn itself out before they get a chance to make their billions…
Nah… Surely not.
*The interview I saw was on YouTube and I can’t find it again for some reason. Here’s the very unbiased Jerusalem Post making the same point.
